[선형대수학] 삼중곱의 확장
2022. 4. 13. 13:02ㆍ❎ Mathematic/Linear Algebra
3차원의 벡터 3개를 곱하려면 어떻게 해야 할까?
공식을 유도할 수 있을까?
유도 과정을 식으로 옮겼다.
천천히 즐기시길!
외적은 결합 법칙, 교환 법칙이 성립되지 않는다.
따라서 이렇게 처음할 때부터, 괄호 등의 제한을 두고 시작한다.

벡터 b와 벡터 c를 먼저 외적 한 후, 벡터 a를 그 위에 외적 한다.
첫 번째 부분만 외적한 후, 결과를 확인하면 나머지는 자연스럽게 알 수 있다.
따라서 첫 번째 부분만 살펴보자.

식을 간단하게 만들기 위해 식에 변화를 주었다.

전체적인 외적 형태는 다음과 같을 것이다.

삼중곱 공식 유도 결과
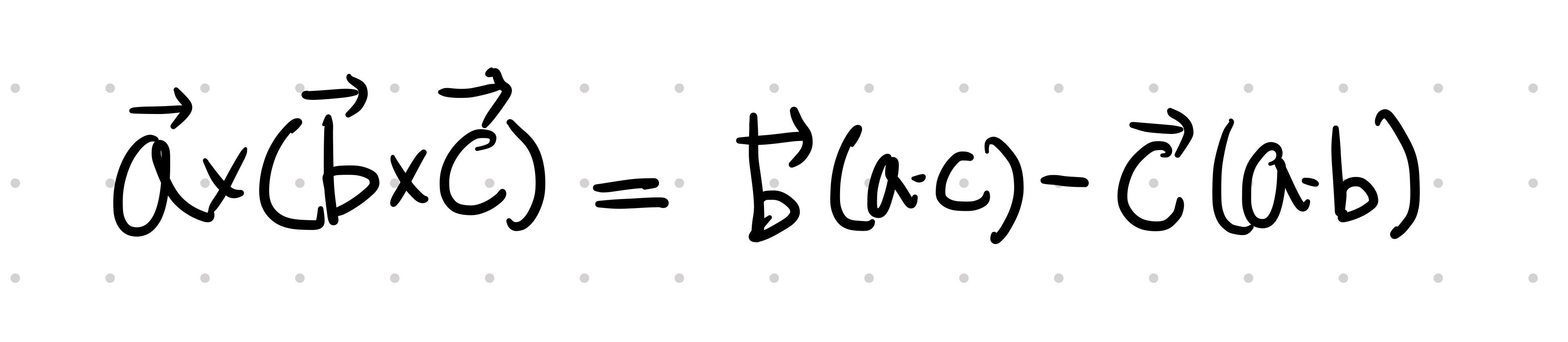
'❎ Mathematic > Linear Algebra' 카테고리의 다른 글
| [선형대수학] 행렬 벡터의 곱 (0) | 2022.06.18 |
|---|---|
| [선형대수학] 평면 사이의 거리 구하기 (0) | 2022.04.25 |
| [선형대수학] 점과 평면 사이의 거리 (0) | 2022.04.15 |
| [선형대수학] 평면 방정식의 법선벡터 (0) | 2022.04.14 |
| [선형대수학] 내적과 외적의 비교/직관 (0) | 2022.04.12 |