[선형대수학] 내적과 외적의 비교/직관
2022. 4. 12. 20:51ㆍ❎ Mathematic/Linear Algebra
선형대수학의 기본인 내적과 외적을 어제 공부했다.
이제 내적과 외적의 의미를 좀 더 확장시켜 보자.
1) 첫 번째 직관 : 내적
"벡터 a 와 벡터 b의 방향이 얼마나 같냐" 그것이 문제로다.
벡터 a, 벡터 b 를 내적 하면 다음과 같다는 결과를 이전에 배웠다.

그렇다면 실제 도형 측면에선 이 수식이 어떻게 작용할까?
다음 그림을 보자.
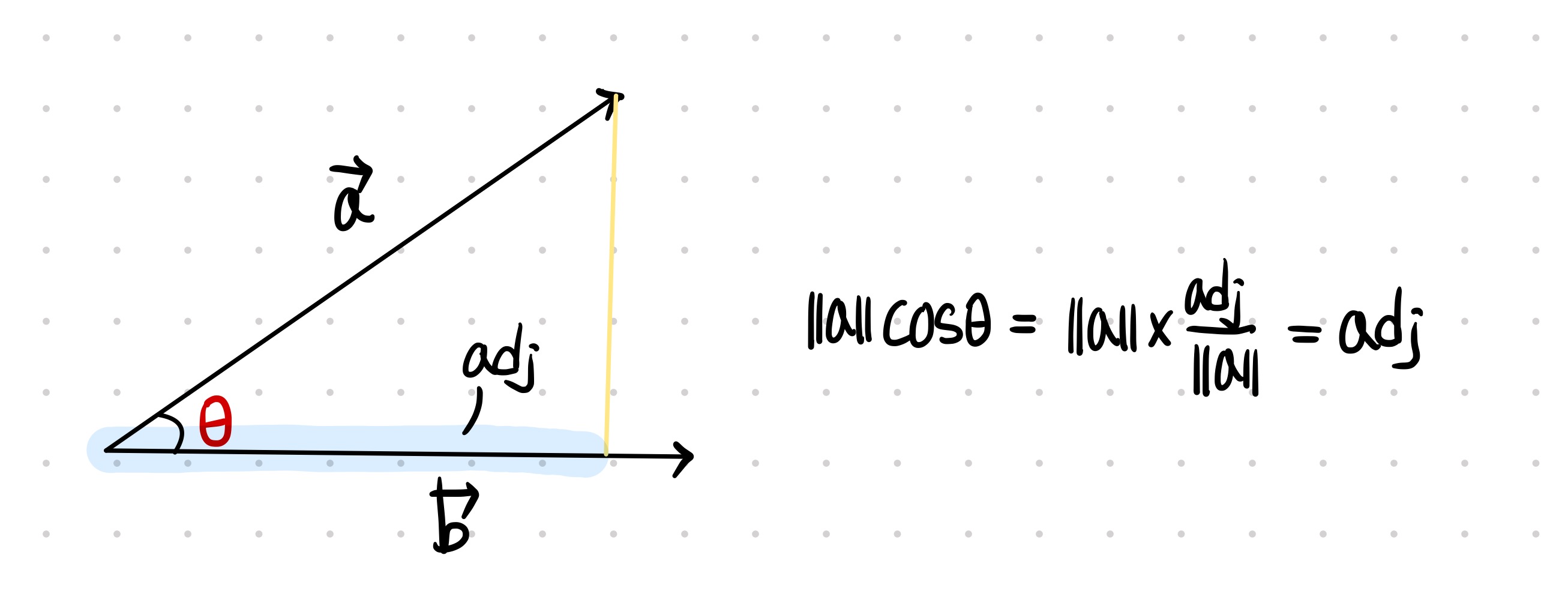
우리가 처음 떠올렸던 수식은 이제 밑의 수식으로 변했다.

즉, 코사인의 값이 얼마나 크냐 ( 벡터 a와 벡터 b의 방향이 얼마나 같냐 )에 따라 a, b의 내적 값이 크게 달라짐을 알 수 있다. 내적은 a, b의 방향이 비슷한 정도에 영향을 많이 받는다.
2) 두번째 직관 : 외적
벡터 a와 벡터 b가 떨어질수록 값이 커진다.
a, b의 외적한 벡터의 길이는 다음 수식을 따른다.
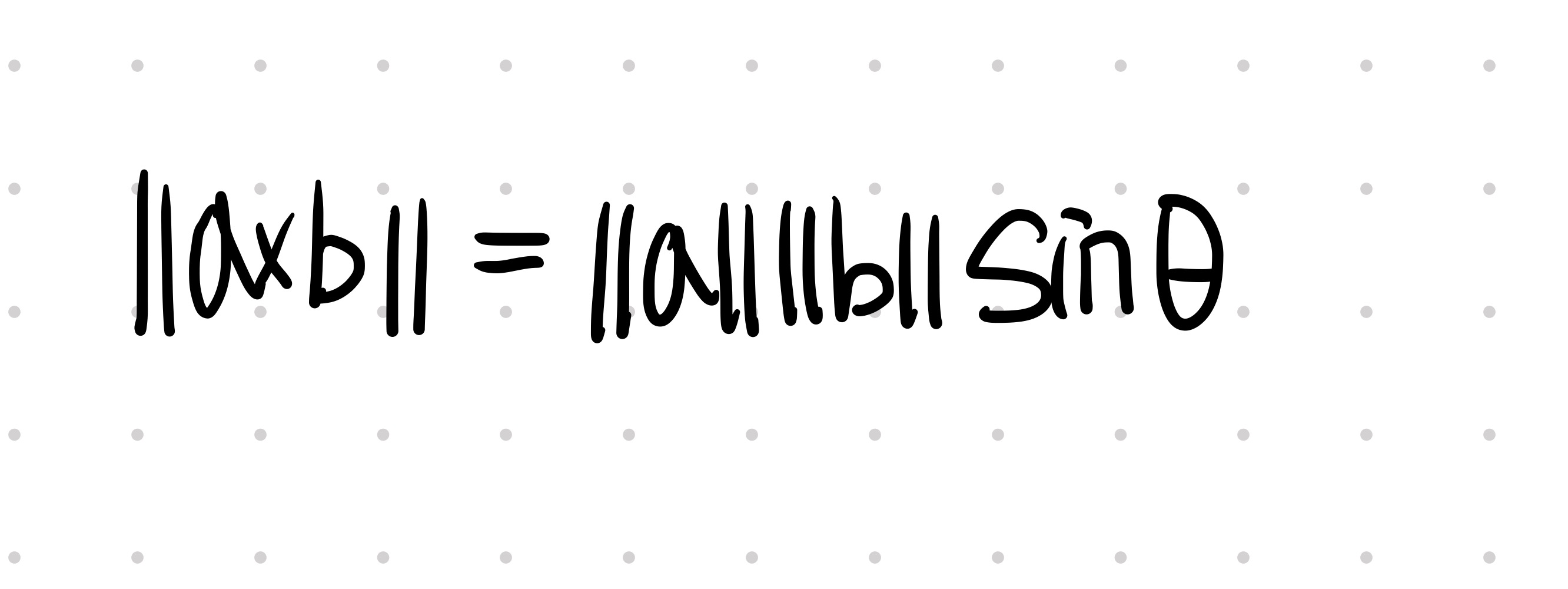
이제 수식을 도형적인 측면에서 접근해볼까?
수식을 풀면, a/b 외적은 b의 길이와 Lin의 곱이 된다.

즉, a와 b의 방향이 다를수록 외적 값이 커짐을 알 수 있다.
3) 외적의 또다른 해석, 평행사변형 넓이
높이와 밑변의 곱이라면... 넓이 아닌가?
평행사변형의 넓이를 구하고 싶다. 외적으로 어떻게 구할 수 있을까?
한번 생각해보시길.

이전에 유도한 Lin 을 그대로 차용해서 높이를 구해주면 된다.
평생 사변형의 넓이는 높이 X 밑변 이다.
이는 외적도 마찬가지이므로, 외적만으로 평행사변형을 구할 수 있다.

'❎ Mathematic > Linear Algebra' 카테고리의 다른 글
| [선형대수학] 행렬 벡터의 곱 (0) | 2022.06.18 |
|---|---|
| [선형대수학] 평면 사이의 거리 구하기 (0) | 2022.04.25 |
| [선형대수학] 점과 평면 사이의 거리 (0) | 2022.04.15 |
| [선형대수학] 평면 방정식의 법선벡터 (0) | 2022.04.14 |
| [선형대수학] 삼중곱의 확장 (0) | 2022.04.13 |