2022. 7. 24. 12:17ㆍ❎ Mathematic/Linear Algebra
이번 포스팅에선, R3 열공간의 평면식을 구해보도록 하겠습니다.
열공간, 기약 행 사다리꼴 행렬 개념을 모르신다면, 학습하고 오시는 걸 추천드립니다.
목차
📃 행렬 정의, 열공간의 기저 구하기
📃 열공간의 기저로 평면식 구하기
행렬 정의, 열공간의 기저 구하기
📌 행렬 정의
행렬 A(MxN)를 정의합니다.

📌 행렬 A를 기약 행 사다리꼴 행렬로 변환합니다.
변환 이유는, pivot 행렬을 구하기 위함입니다.
(1) 실행

(2) 실행

(3) 실행
기약 행 사다리꼴 행렬이 완성되었습니다.
pivot 행렬은 첫 번째 열 벡터와 두 번째 열 벡터입니다. 이 두 개의 행렬로 다른 두 개의 행렬을 모두 나타낼 수 있습니다.

예를 들어,
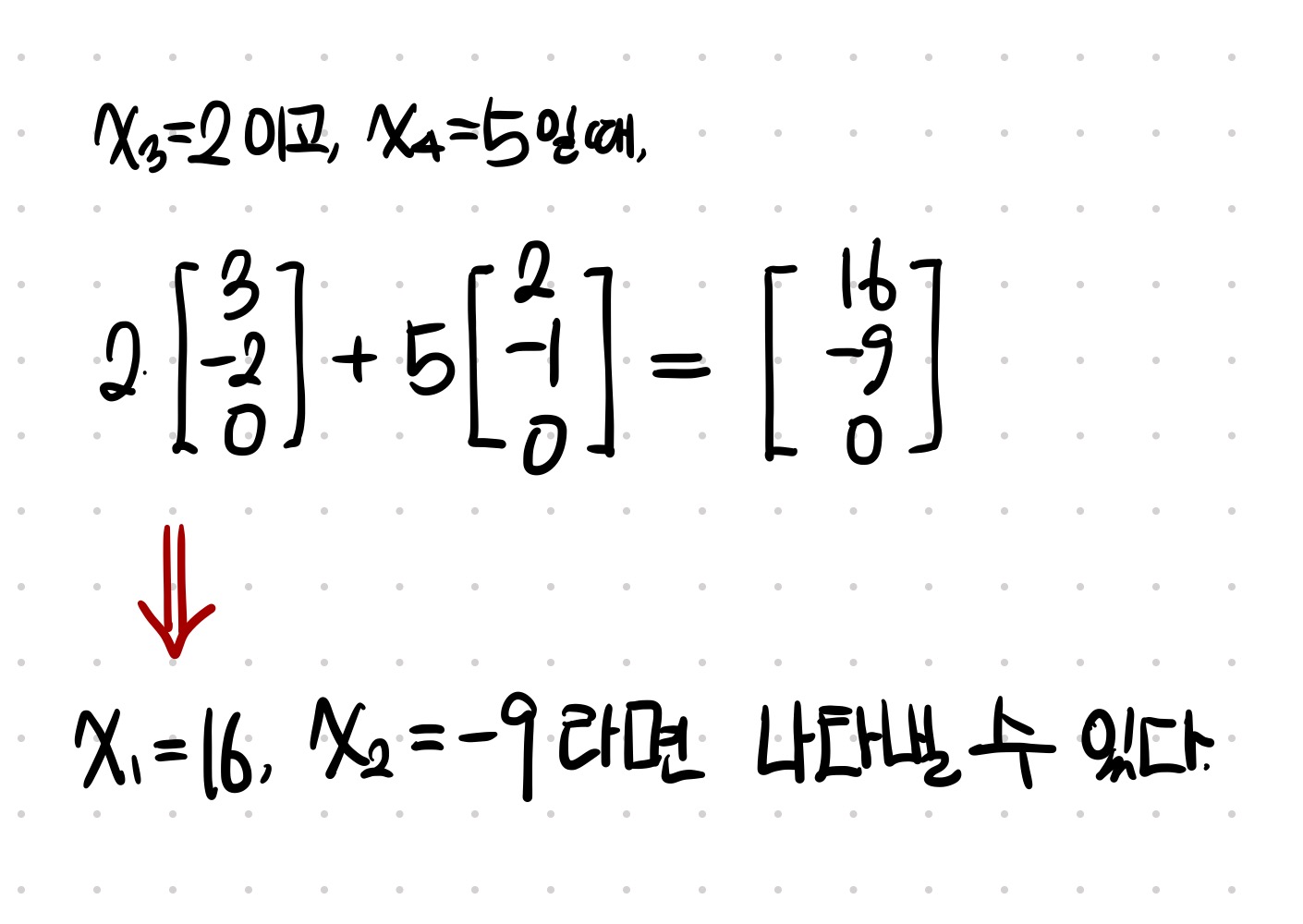
이에 따라 V1, V2는 선형독립이며, 행렬 A의 열공간의 기저라고 할 수 있습니다.
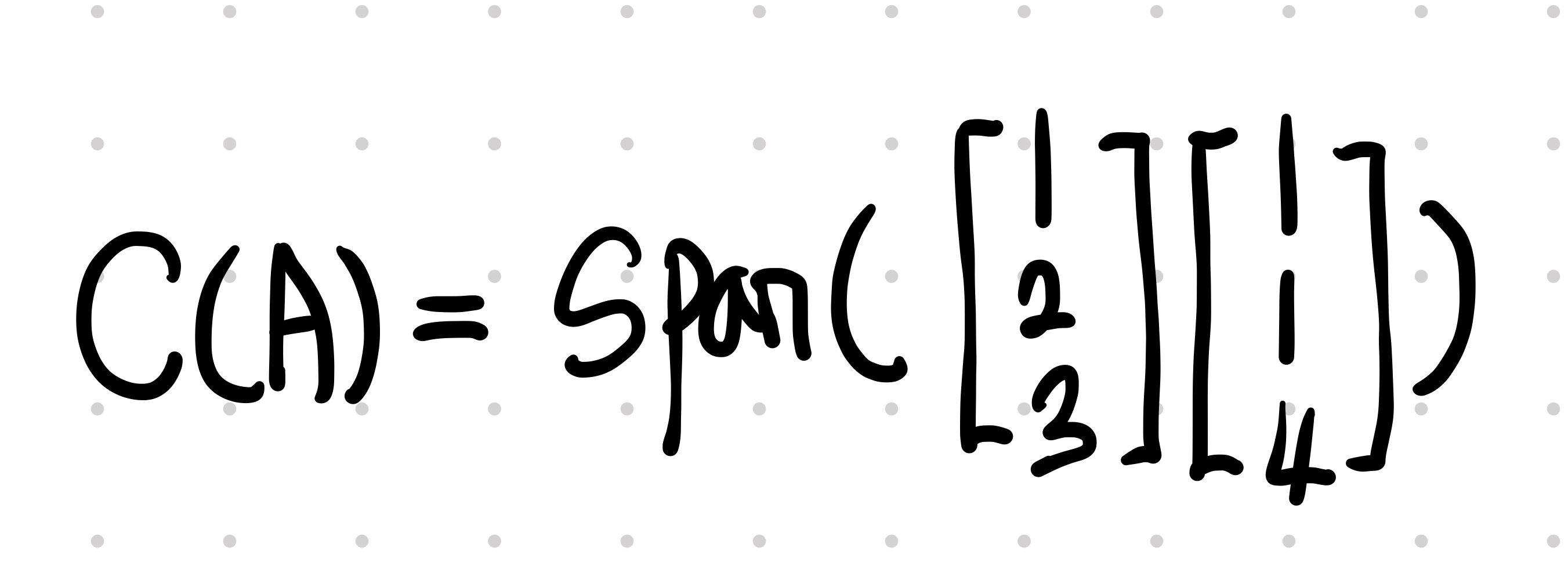
열공간의 기저로 평면식 구하기
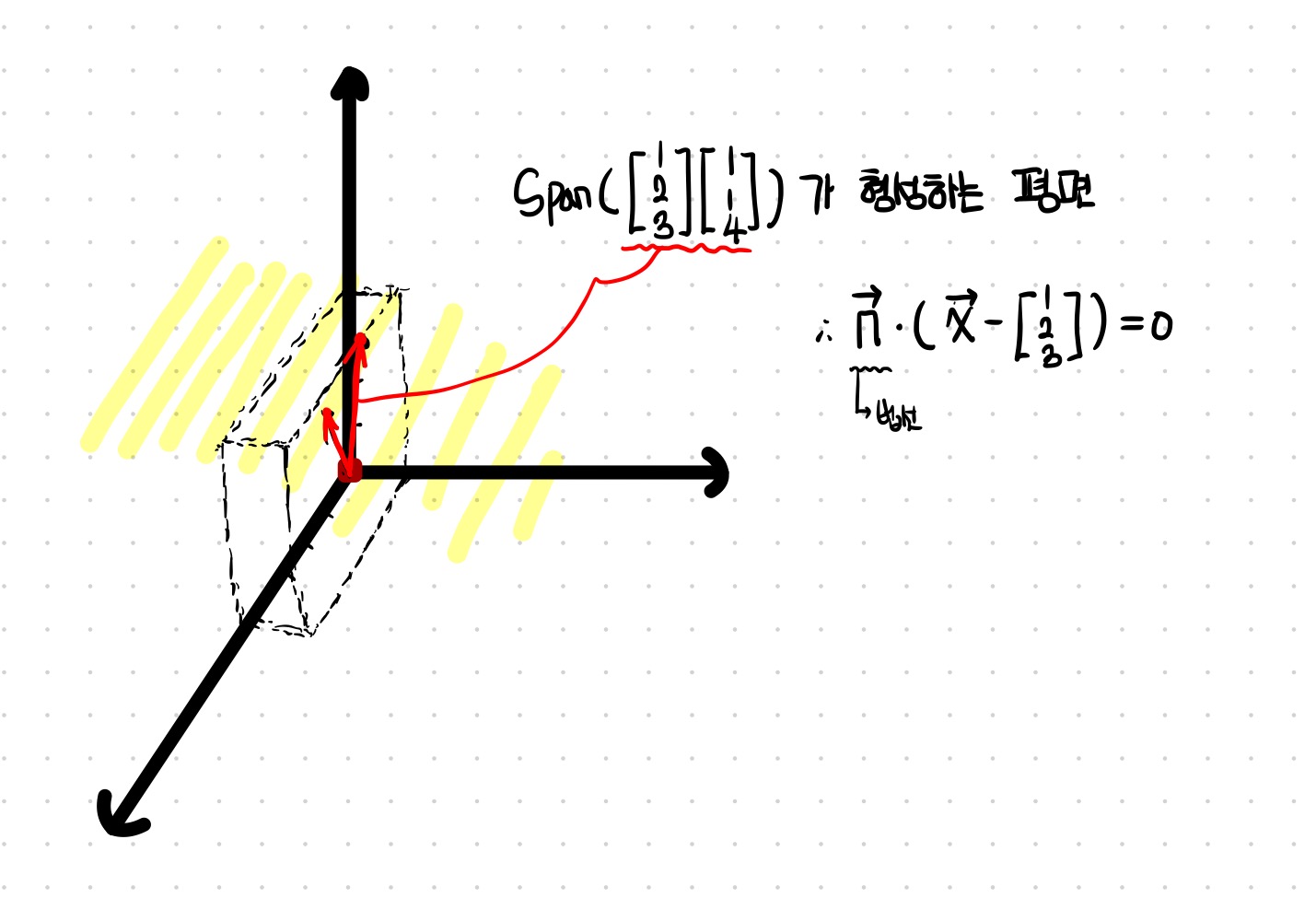
📌 열공간의 기저를 그래프를 통해 나타내 봅니다.
다음과 같이 3차원 그래프에 표현할 수 있습니다. 이 둘의 벡터로 나타낼 수 있는 모든 벡터의 집합은 하나의 평면(노란 형광 영역)을 나타낼 것입니다. 평면식은 어떻게 구할 수 있을까요? 법선벡터와 평면위의 벡터를 내적하면 0이 나온다는 것을 이용하면 구할 수 있습니다.
📌 법선 벡터 구하기
법선 벡터는 평면의 직각일 것입니다.
기저 벡터의 외적은 곧 직각 벡터를 반환하며, 이를 이용하면 법선 벡터를 구할 수 있습니다.
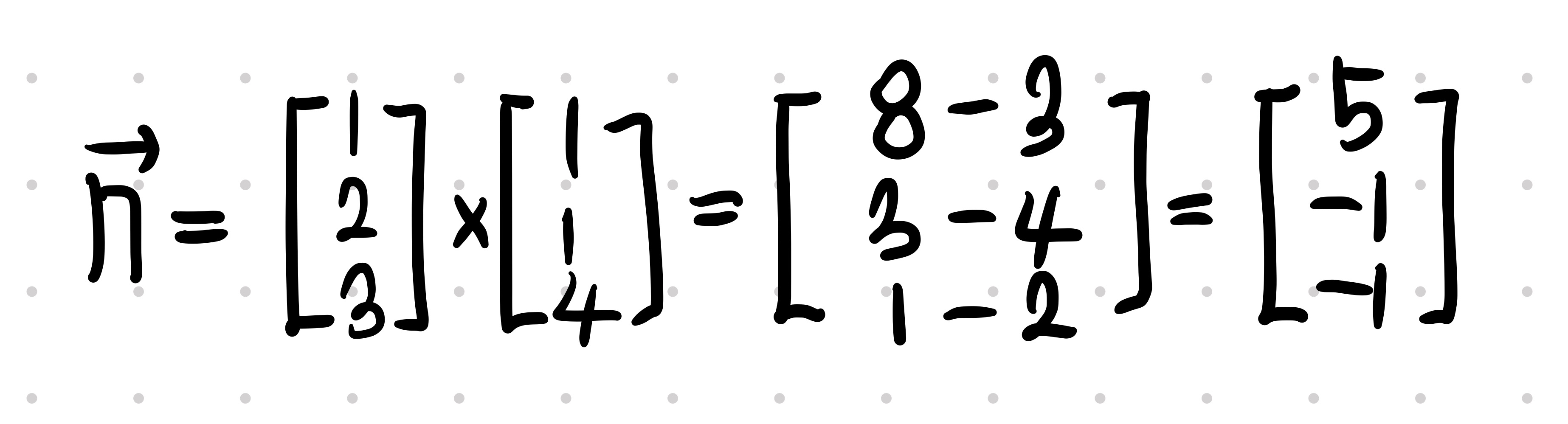
📌 법선 벡터를 평면식에 대입
구해진 법선 벡터를 평면식에 대입해줍니다.
아주 간단한 벡터들의 내적이 보입니다.
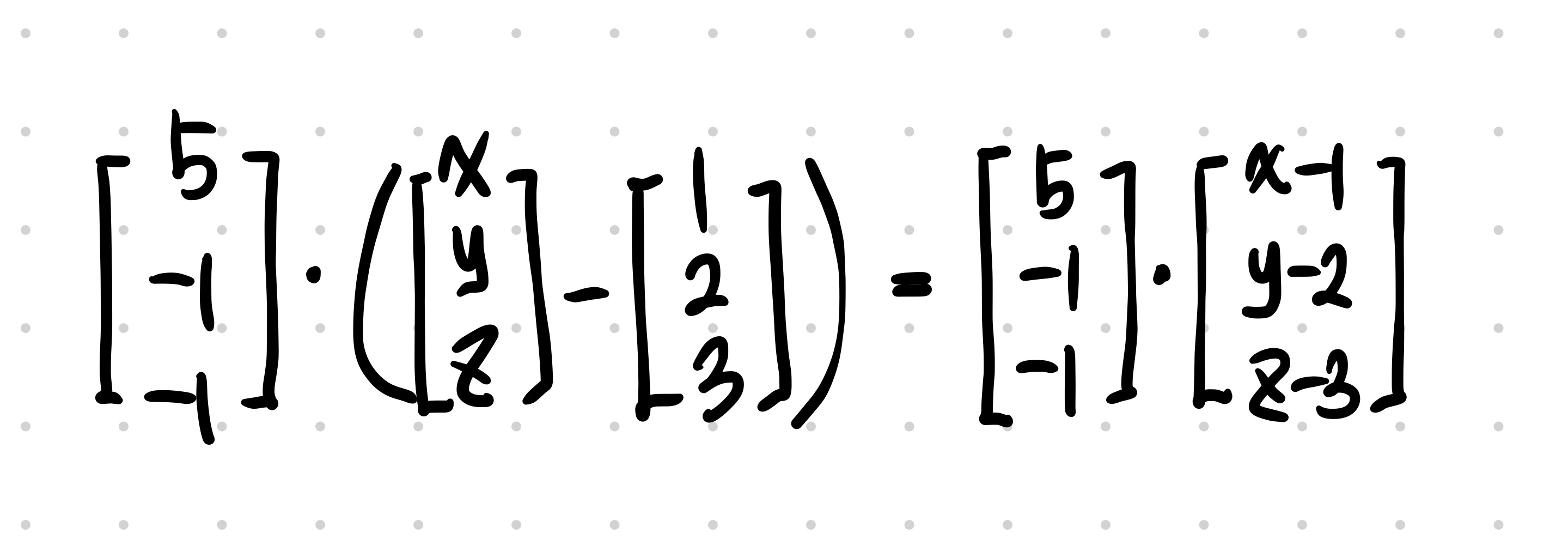
벡터 내적을 풀어주면 다음과 같은 식을 도출됩니다.
잘 정리하면, x, y, z로 구성된 이쁜 평면식을 구해낼 수 있습니다.
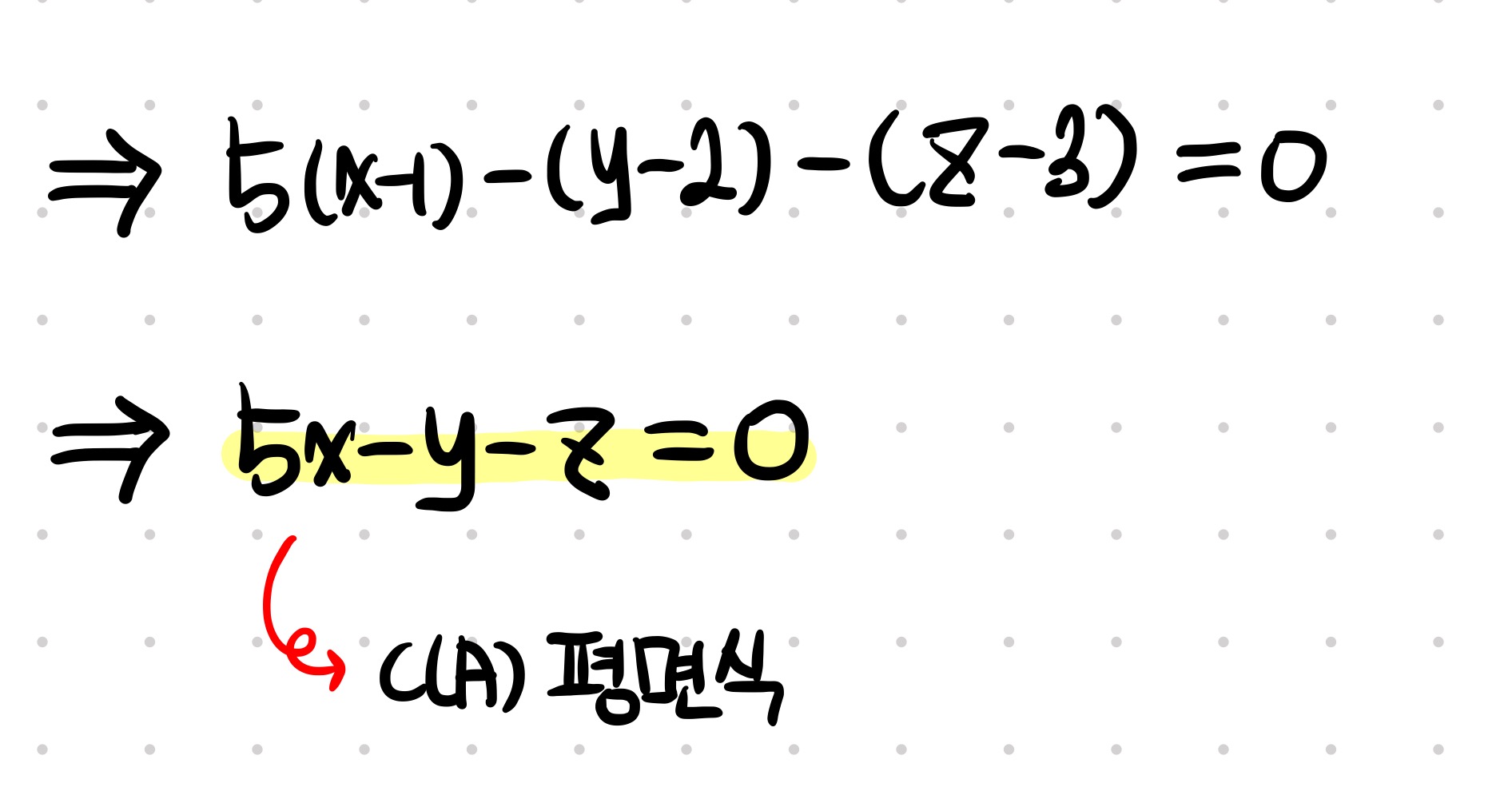
📌 복습
R3 열공간의 평면식을 구하는 순서는 다음과 같았습니다.
(1) 열공간의 기저 구하기
(2) 법선 벡터 구하기
(3) 평면식에 대입하기
(4) 식을 풀어주기
평면식을 구하는 방법은 하나 더 있습니다(더 간편). 이는 다음 포스팅에서 다루겠습니다.
고생하셨습니다.
'❎ Mathematic > Linear Algebra' 카테고리의 다른 글
| [선형대수학] 행렬의 열공간 (Column Space of a Matrix) (0) | 2022.07.22 |
|---|---|
| [선형대수학] 영공간과 선형독립 간의 관계 (Relation of null space to linear independence of columns) (0) | 2022.07.05 |
| [선형대수학] 행렬의 영공간 계산하기(Calculationg the null space) (2) | 2022.06.25 |
| [선형대수학] 행렬의 영공간 (Null space of a matrix) (1) | 2022.06.19 |
| [선형대수학] 행렬 벡터의 곱 (0) | 2022.06.18 |