2022. 7. 22. 14:30ㆍ❎ Mathematic/Linear Algebra
이번 포스팅에선 행렬의 열공간 (Column Space of a Matrix)에 대해 알아보겠습니다. 만약 영공간에 대한 개념을 모르신다면 아래의 포스팅들을 보고 와 주시길 바랍니다.
포스팅의 목표: 행렬의 열공간 개념을 이해하고 설명할 수 있다.
[행렬의 영공간이란?]
[선형대수학] 행렬의 영공간 (Null space of a matrix)
행렬의 영공간에 대해 알아보는 포스팅입니다. 행렬은 어느정도 이해가지만, 영공간은 대체 무슨 말인지 모르겠습니다. 영공간을 이해하기 위해선 먼저 부분 공간에 대한 복습이 이뤄져야 합니
mengu.tistory.com
[행렬의 영공간 계산하기]
[선형대수학] 행렬의 영공간 계산하기(Calculationg the null space)
행렬의 영공간이란? 행렬 A와 곱하여 영벡터를 만드는 모든 벡터 x의 집합입니다. 자세한 개념이 생각 안 나신다면 저번 포스팅을 보며 복습해주세요. https://mengu.tistory.com/82?category=937657 [선형대
mengu.tistory.com
📌 행렬 A와 열 벡터
행렬 A(MxN)를 정의해보겠습니다.

행렬 A의 열들을 하나의 벡터로 생각하면 어떨까요?
행렬 A = [V(1), V(2), V(3), V(4) ... V(n)]

📌 행렬 A의 열공간
행렬 A의 열공간은 행렬 A의 열 벡터들의 생성(span)을뜻합니다.
즉, 열 벡터들의 선형 결합으로 탄생할 수 있는 모든 벡터들의 집합이라 보시면 됩니다.

<행렬 A의 열 벡터의 생성>

📌 행렬 A의 열공간 유효성
열공간도 하나의 부분 공간입니다.
따라서 부분 공간의 유효성을 검증해야 합니다.
(1) 0 벡터를 포함하는가?
(2) 벡터 a와 벡터 b가 C(A)에 포함된다면, 벡터 a + 벡터 b도 C(A)에 포함되는가?
(3) 벡터 a가 C(A)에 포함된다면, c*벡터 a도 C(A)에 포함되는가?
✔ 첫 번째 조건 : 영벡터 포함
선형 결합의 계수인 C1, C2, C3 ... Cn이 만역 전부 0이라면, Span(...)은 0벡터를 포함합니다.

✔ 두 번째 조건
벡터 a와 벡터 b가 C(A)에 포함된다고 가정합니다.
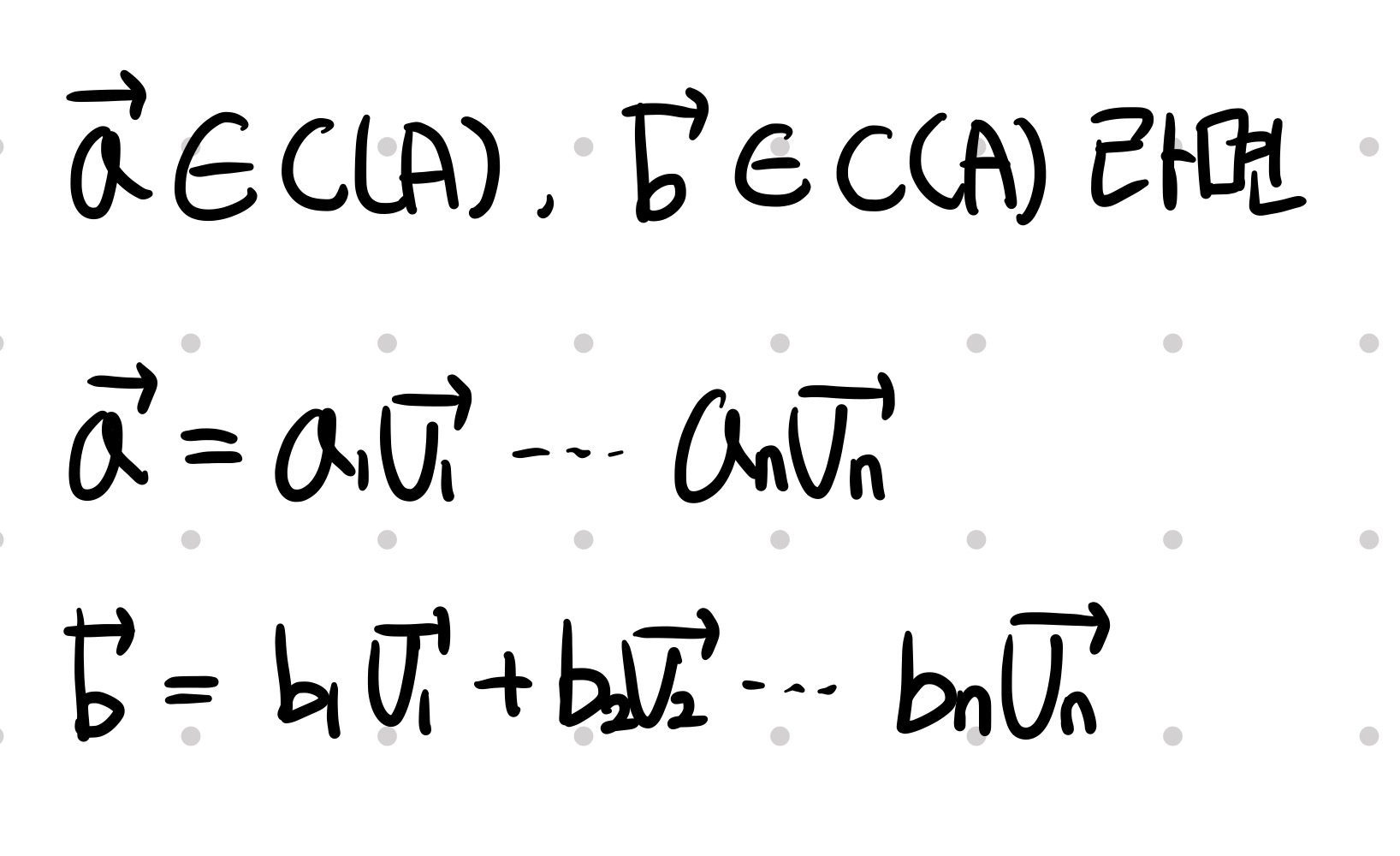
식을 나열하면, 본래의 선형 결합과 똑같이 재현할 수 있습니다. 따라서 두 번째 조건도 만족합니다.
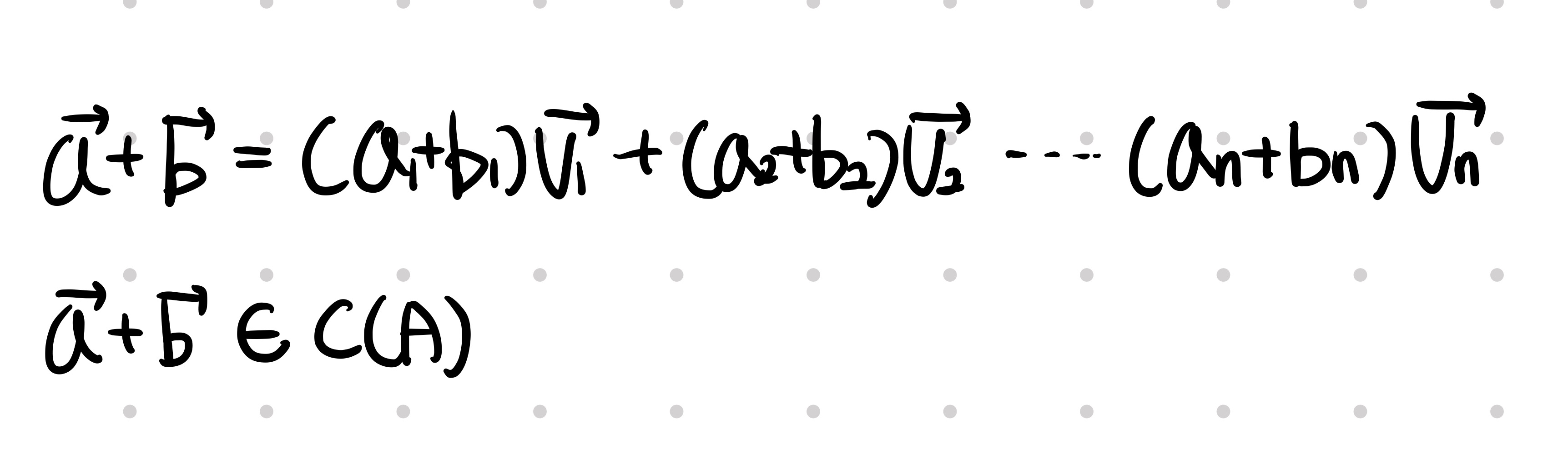
✔ 세 번째 조건
벡터 a가 C(A)에 속한다고 가정합니다.
S*벡터 a를 나열할 경우, 마찬가지로 선형 결합(span 식)으로 나타낼 수 있습니다.
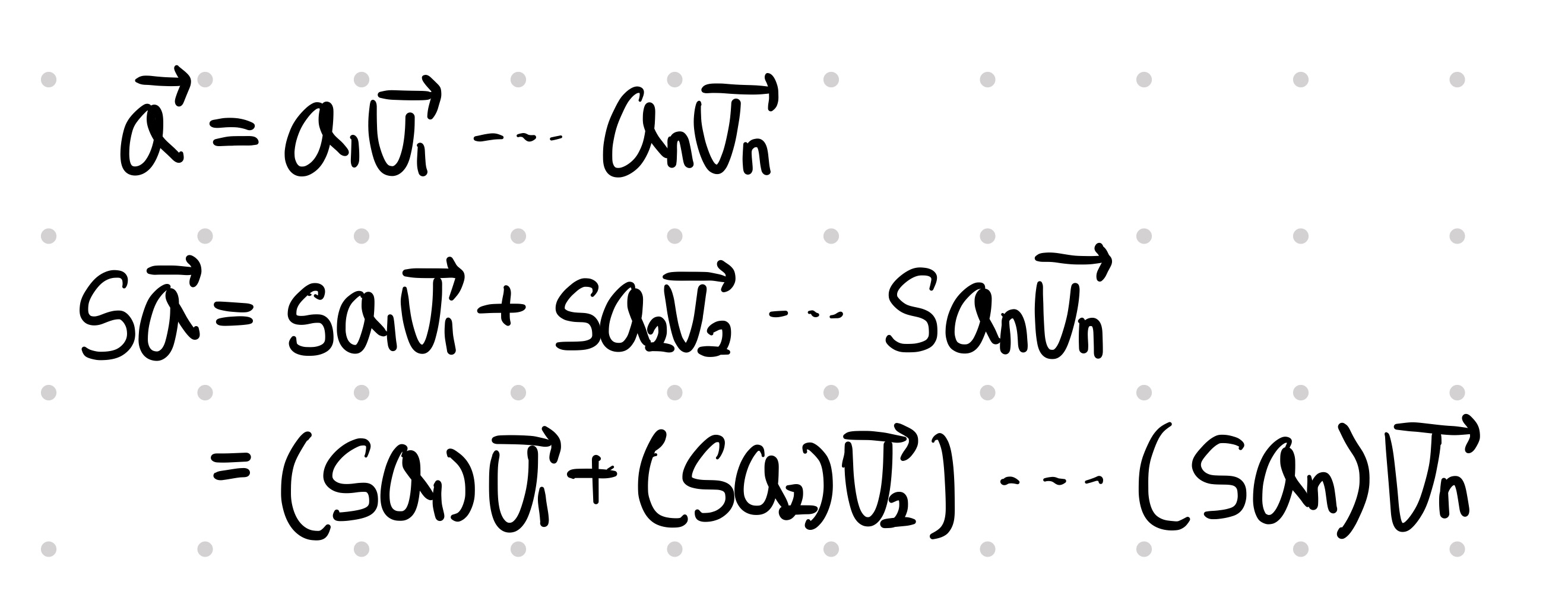
이에 따라 S*벡터 a도 C(A)에 속하게 되므로, 세 번째 조건도 만족합니다.
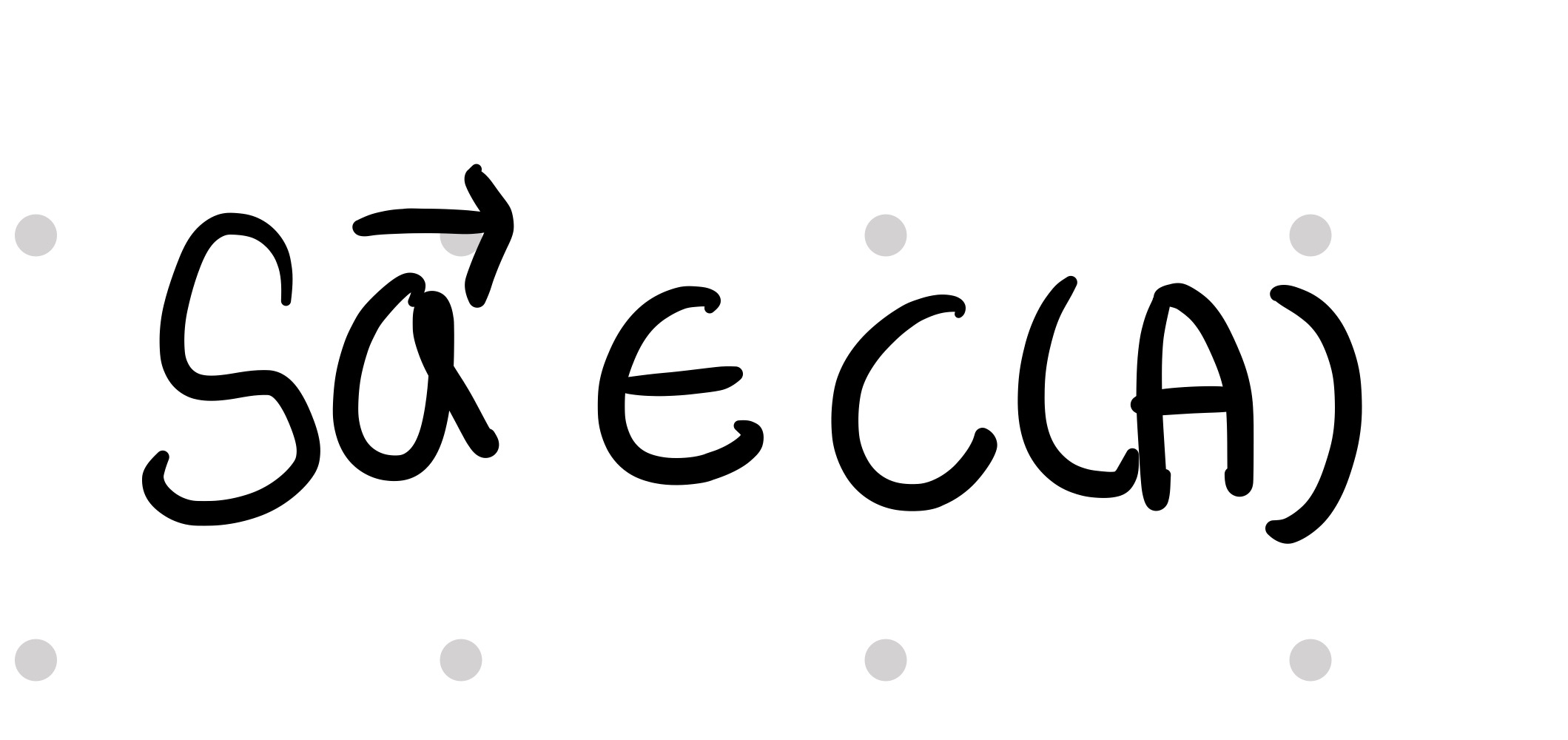
첫 번째, 두 번째, 세 번째 조건을 모두 만족했습니다.
따라서 행렬 A의 열공간은 유효하다고 할 수 있습니다.
📌 행렬 A 열공간을 다르게 표현해보기
행렬 A의 열공간은 이렇게 표현할 수도 있습니다.
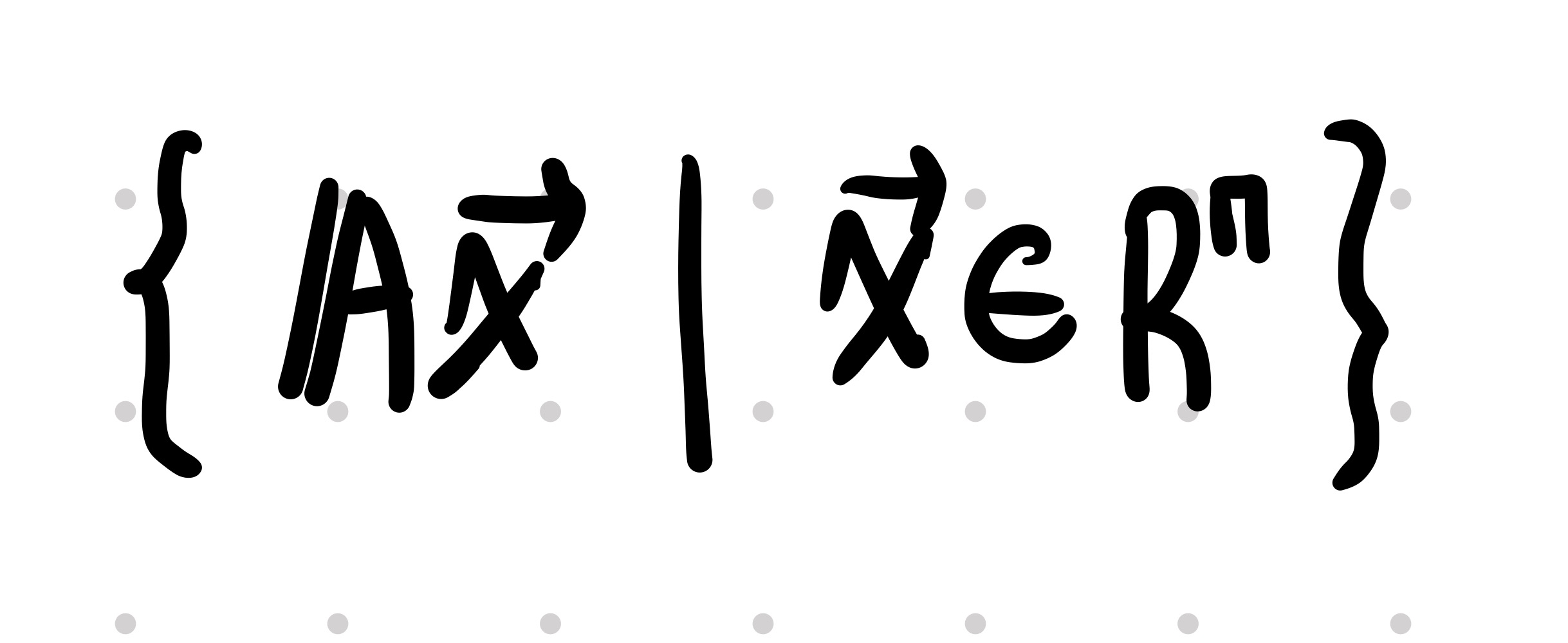
위의 식을 풀면 다음과 같습니다.
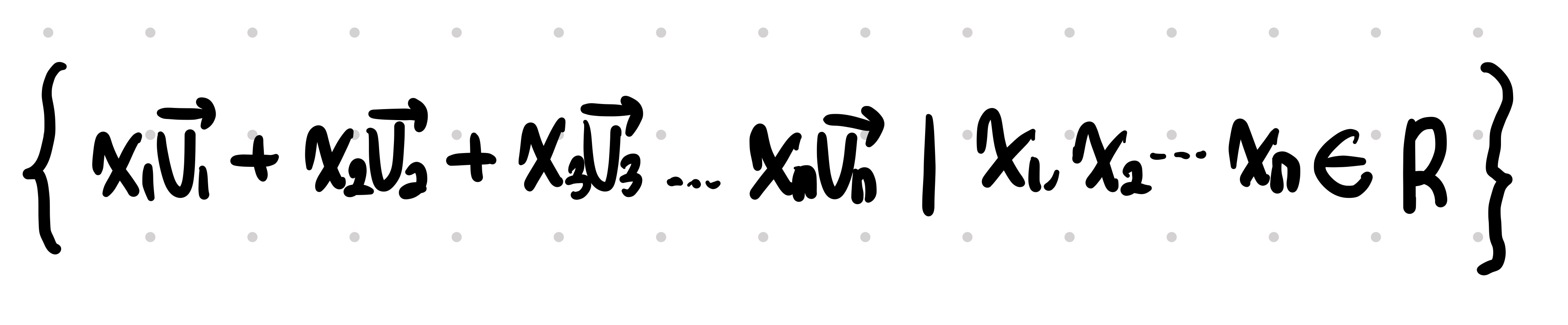
위의 집합을 벡터와 벡터의 곱으로 나타냈습니다.
그런데 이 모습 어디서 보지 않았나요? 그렇습니다. 행렬 A의 열 벡터 들을 선형 결합시킨다면 이런 모양이 나올 것입니다.
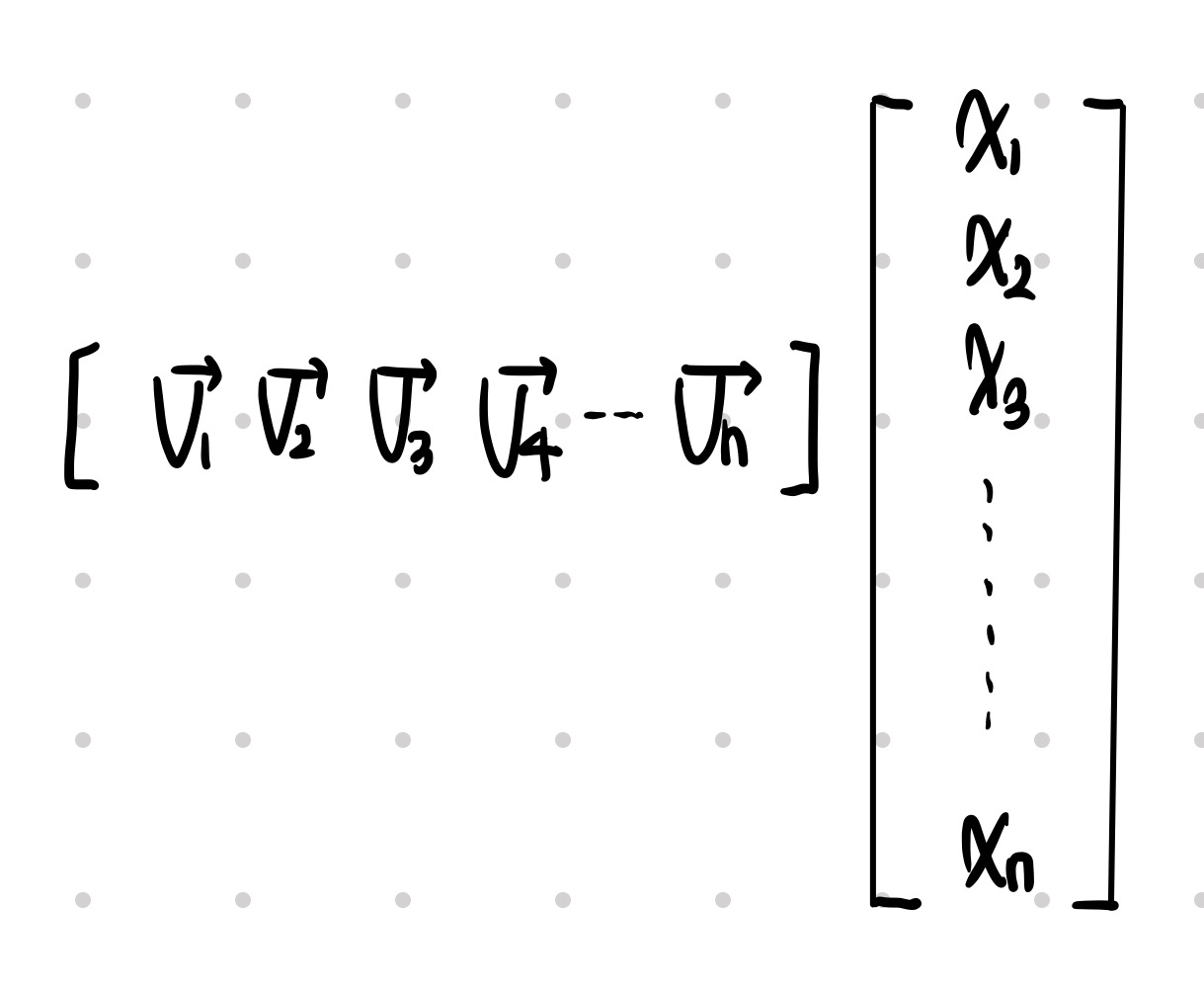
간단한 문제입니다.
생각해보고 맞으시길 바랍니다.

답: 그런 벡터 x는 존재하지 않습니다.
해설: 애초에 A*x가 C(A)이기 때문.
지금까지 행렬의 열공간에 대해 알아보았습니다.
수고하셨습니다.
'❎ Mathematic > Linear Algebra' 카테고리의 다른 글
| [선형대수학] R3 열공간의 평면식 구하기 (0) | 2022.07.24 |
|---|---|
| [선형대수학] 영공간과 선형독립 간의 관계 (Relation of null space to linear independence of columns) (0) | 2022.07.05 |
| [선형대수학] 행렬의 영공간 계산하기(Calculationg the null space) (2) | 2022.06.25 |
| [선형대수학] 행렬의 영공간 (Null space of a matrix) (1) | 2022.06.19 |
| [선형대수학] 행렬 벡터의 곱 (0) | 2022.06.18 |